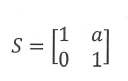게임 프로그래머

이동 변환을 위한 아핀 공간

임의의 벡터 (x, y)를 지정한 크기 (a, b)만큼 이동시키는 기능은 행렬의 덧셈으로 구할 수 있음

하지만 행렬곱으로는 구할 수 없기 때문에 이동 선형 변환은 없음

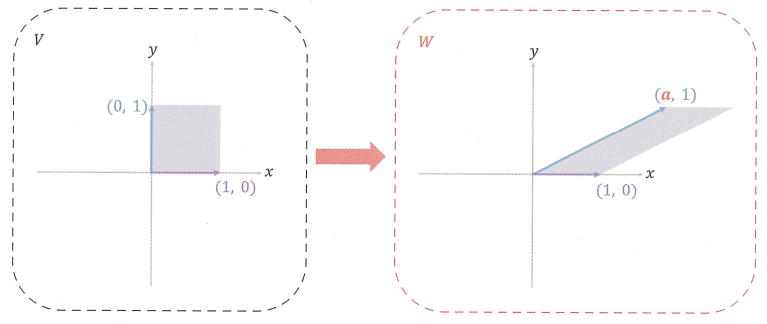
전단 변환의 성질을 활용해 공간의 차원을 하나 더 늘려 특정 조건하에 이동 구현이 가능

y값에 1을 고정한 상태에서 전단 변환을 적용하면 다음과 같은 결과가 나옴

y = 1이라는 조건 하에 a 만큼 미는 전단 변환의 결과는 1차원의 이동 변환 x + a로 활용

마찬가지로 2차원에 적용하여 3차원 공간으로 확장한 후 z 값을 1로 고정한 이동 변환 행렬을 사용

• 이동 변환행렬에서 주의할 점은 마지막 차원 값이 1이어야 한다는 것

아핀(Affine) 공간 : 벡터 공간에서 이동을 위해 마지막 차원 값을 1로 한정한 부분 부분 공간

이동 변환에 맞춰서 크기 변환행렬과 회전 변환행렬도 3차원으로 늘려 설계한 선형 변환을 아핀 변환이라고 함

임의의 벡터 (x, y, 1)을 아핀 변환행렬에 곱한 결과는 마지막 차원 값이 1이 되므로 아핀 공간에 닫혀 있음

아핀 공간의 구성 요소

점

마지막 차원 값이 1인 아핀 공간의 원소

점이 지니는 성질은 행렬 곱을 사용해 이동이 가능하므로 가상 공간이 이동하려면 물체는 점으로 구성되어야 함

점과 점을 더하는 수식은 성립하지 않는데, 마지막 차원 값이 2가 되어 아핀 공간을 벗어나기 때문

이동 벡터

아핀 공간 내의 이동을 지정하기 위해 사용

아핀 공간의 점과 점 간의 최단 거리로 정의됨

아핀 공간의 점에 이동 벡터를 더한 결과는 아핀 공간의 다른 점에 대응됨

P1 + v = P2

점과 점의 뺄셈으로 이동 벡터를 만들 수 있음

v = P2 - P1

v는 P1에서 P2로 향하는 벡터를 의미

이동 벡터는 마지막 차원 값이 항상 0이 됨

아핀 결합

점과 점을 더할 때 그대로 더하는 것이 아닌 스칼라를 곱해 더하면 특정 조건에서 새로운 점을 생성하는 것이 가능해짐

aP1 + bP2 = (ax1 + bx2, ay1 + by2, a+b)

두 점의 선형 결합 결과가 점이 되려면 a+b가 1이 되어야 함

여러 개의 점을 결합해 새로운 점을 생성하는 수식을 아핀 결합이라고 함

두 점의 결합

aP1 + (1-a)P2 = P', (a+b = 1를 이용)

a(P1-P2) = P' - P2

au = v 이므로, u와 v는 서로 평행한 벡터이기 때문에 두 점의 아핀 결합으로 생성되는 점은 P2에서 P1을 지나는 직선 상에 위치함을 보장받음

이 수식을 직선의 방정식이라고 함

직선(Line)은 두 점의 양쪽 방향으로 무한히 뻗어나가는 선의 형태를 의미하며, 추상적인 선의 성질을 표현할 때 사용

반직선(Ray)은 지정한 위치에서 한쪽 방향으로만 뻗어나가는 선

• Raycasting : 전방에 물체가 있는지 탐지하기 위해 지정한 위치에서 특정한 방향으로 반직선을 던져 맞닿는 물체를 탐지하는 기능
• Raytracing : 화면에 도달한 빛의 경로를 거꾸로 추적해 시뮬레이션하여 사실적인 이미지를 만들어내는 기법

선분(Line Segment)는 시작점과 끝점의 위치가 정해져 있는 선

• 화면에 선을 그리려면 무한이라는 추상적인 개념을 배제하고 명확하게 선분의 형태로 정보가 제공되어야 함

선 그리기 알고리즘

벡터를 모니터의 점으로 표현

모니터 화면의 좌표계는 스크린 좌표계를 사용

• y축이 아래쪽을 향함
• 실수가 아닌 정수를 사용

픽셀 : 스크린 좌표와 색상에 대응하는 화면의 구성 요소

• 화면에 무언가를 표현하기 위해서는 반드시 색상이 함께 지정돼야 함

픽셀화(Rasterization) : 실수로 표현된 벡터 좌표를 정수로 변환한 후 색상을 부여하는 과정

• 화면 해상도의 크기가 짝수인 경우 원점을 픽셀로 표현하려면 중앙의 네 픽셀 중 하나를 선택하는 규칙을 정해야 함
• 반대로 스크린 좌표를 벡터로 변환할 때는 픽셀이 가로 세로로 [0, 1] 범위 영역을 가지기 때문에 이 중 해당 영역을 대표하는 벡터를 선정해야 함

선 그리기 알고리즘

스칼라 a 값의 범위를 0부터 1까지 범위를 늘려가면서 벡터를 생성하는 것은 비효율

• 모니터 화면은 정수 좌표로 구성되어 있기 때문에 하나의 픽셀에 대응되는 다수의 벡터가 생성되기 때문

Bresenham's Algorithm은 화면은 8등분 영역으로 구분한 후 각 영역별로 그려내는 방식을 사용

단순하고 빠르지만 화면을 벗어나는 큰 값이 들어오더라도 알고리즘을 수행해야 하는 단점이 있음

먼저 1팔분면을 생각하면 스크린 좌표계에서 y축이 아래로, x축이 오른쪽으로 증가

첫 픽셀이 (x0, y0)일 때 두 번째 픽셀은 y값이 y0 아니면 y0 + 1이므로 중간값인 0.5를 활용 (x0 + 1, y0 + 0.5)

(x0 +1, y0 + 0.5)가 직선의 방정식보다 위에 있는지 아래에 있는지 판별하여 위에 있으면 y0 + 1, 그렇지 않으면 y0로 픽셀을 찍음

다른 팔분면도 원리는 동일

라인 클리핑 알고리즘(cohen-sutherland line clipping algorithm)

Bresenham's Algorithm의 화면을 벗어나는 큰 값이 들어오더라도 알고리즘을 수행해야 하는 문제를 예방

선분이 가진 성질을 유지하면서 지정된 영역에 맞는 데이터로 재설정하는 작업을 클리핑이라고 함

입력된 선분을 그릴 영역을 화면과 그 바깥 영역을 포함해 총 9개로 설정

각 영역마다 상위 두 비트는 상하 정보, 하위 두 비트는 좌우 정보를 담아 4비트로 고유한 값을 부여

0000 영역은 눈에 보이는 화면 영역을 의미

선분을 구성하는 시작점과 끝점이 모두 0000 영역에 있다면 클리핑 없이 선을 그리고, 그렇지 않다면 클리핑 해야 함

• 화면 안에 위치해서 자를 필요가 없는 경우
  • 두 점을 & 연산하면 0보다 큼
  • 두 점을 & 연산하여 0이 나올 경우 클리핑을 하면 다시 & 연산의 결과가 0 이상의 값이 나옴
• 화면 밖에 위치해 있어서 그릴 필요가 없는 경우
• 화면을 가로 질러서 화면에 유효한 영역으로 잘라내야 하는 경우(클리핑)

선형성: 예측 가능한 비례 관계

선형성 : 직선의 형태를 띠는 성질, 두 집합의 순수한 비율로 구성된 1차적 대응 관계를 의미

수학에서의 선형성은 가법성과 1차 동차성을 모두 만족하는 함수의 성질

• 가법성 : f(x1 + x2) = f(x1) + f(x2)
• 1차 동차성 : f(kx) = kf(x)

벡터 공간의 선형 변환

표준기저벡터의 선형 결합으로 형성된 벡터 공간은 선형성을 지님

벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성되므로 선형성을 지님

이렇게 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환이라고 부름

선형성을 유지시켜주는 선형 함수는 선형 변환이라고 함

행렬

선형 변환의 계산 과정을 체계화하여 손쉽게 계산할 수 있는 편리한 도구

수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블

(x, y)로 구성된 2차원 벡터에서 A는 열벡터, B는 행벡터

선형 변환을 표현할 때는 행과 열의 크기가 같은 정방행렬을 사용

행렬의 기본 연산

행렬과 행렬의 덧셈 : 행렬의 크기가 같은 경우에만 성립

행렬과 스칼라의 곱셈

행렬의 전치 : 행과 열을 바꾸는 작업

행렬의 곱셈 : 행벡터와 열벡터를 각각 곱하는 방식

교환법칙이 성립하지 않음

결합법칙이 가능하고, 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 동일

결합법칙은 그래픽 연산의 계산량을 크게 줄여줌

• 100개의 점으로 구성된 물체가 5번의 선형 변환이 일어날 때, 각 점마다 5번의 행렬 곱이 수행되므로 행렬 곱의 총 횟수는 500
  만약 5번의 선형 변환에 대한 결과 행렬 F를 만들고 각 점에 F만 곱하면 행렬 곱의 총 횟수는 104

행렬의 설계

두 표준기저벡터 (1,0)과 (0,1)이 (a,c)와 (b,d)에 대응되어 변환될 때를 생각해보자

w = x(a,c) + y(b,d) = (ax+by, cx+dy)

표준기저벡터가 정방행렬을 구성하는 열벡터임을 알 수 있음

이를 활용해 원하는 형태로 공간이 변화되도록 행렬을 설계할 수 있음

크기 변환행렬

표준기저벡터 e1을 a배, e2를 b배 변화시키는 행렬

회전 변환행렬

각 theta로 벡터 공간을 회전시키는 회전 변환행렬

전단 변환행렬

두 표준기저벡터 중 하나의 표준기저벡터만 변환하는 행렬

x축 방향으로 a만큼 변환하는 전단 변환행렬

삼각함수의 덧셈 정리

역행렬

항등행렬 : 동일한 공간으로 유지하는 변환을 의미

역행렬 : 행렬곱의 결과가 항등행렬이 나오는 행렬

선형 변환된 벡터 공간을 다시 원 벡터 공간으로 되돌리는 선형 변환

역행렬의 존재를 판별하는 행렬식

행렬식 : 행렬이 역행렬이 존재하는지 파악할 수 있는 수식

행렬식의 값이 0이면 역행렬이 존재하지 않음

두 기저벡터의 기울기가 같아 2차원이 1차원으로 압축됐다고 볼 수 있고, 이는 원 공간의 정보가 소멸되기 때문에 원 벡터 공간으로 변환이 불가능해짐

크기 변환행렬의 역행렬

전단 변환행렬의 역행렬

회전 변환행렬의 역행렬

각 theta 회전했으므로 각 -theta만큼 회전하는 행렬을 구하면 됨

삼각함수의 성질을 이용

cos(-theta) = cos(theta)
sin(-theta) = -sin(theta)

회전행렬과 전치 관계에 있기 때문에 별도로 삼각함수를 사용하지 않아도 전치연산을 적용하여 쉽게 구할 수 있음

행렬 곱의 역행렬

삼각함수

삼각비 : 직각삼각형을 구성하는 세 변에서 각각의 비례관계를 나타낸 것

• sin(theta) = b/c
• cos(theta) = a/c
• tan(theta) = b/a

삼각함수 : 직각삼각형을 데카르트 좌표계 상에 배치하고 사잇각의 범위를 실수 전체로 확장한 대응 관계

삼각함수를 활용하여 반지름이 r인 원주 위의 모든 좌표는 r(cos(theta), sin(theta))에 대응됨

삼각함수의 성질

데카르트 좌표계에서 각도는 x축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를 의미

sin 함수와 cos 함수는 진폭 사이를 일정하게 반복하는 패턴을 띰

sin 함수와 cos 함수는 360' 주기로 반복

y축을 기준으로 cos 함수는 좌우 대칭(짝함수, 우함수), sin은 원점 대칭(홀함수, 기함수)

• cos(-theta) = cos(theta)
  sin(-theta) = -sin(theta)

각의 측정법

삼각함수를 응용할 때에는 각도법 대신 호의 길이를 기준으로 각을 측정하는 호도법(Radian)을 사용

라디안은 호의 길이가 1이 되는 부채꼴의 각을 기준으로 측정

반원의 호는 파이이므로 약 3.14인데, 호의 길이를 1로 설정하면 1라디안은 약 57.29'

1(rad) = (180/파이)'

삼각함수를 활용한 물체의 회전

회전은 x와 y값이 함께 영향을 미치기 때문에 x축과 y축을 분리해 독립적으로 계산할 수 없음

2차원 실벡터 공간은 두 표준기저벡터 e1, e2로 두고, 공간에 속한 모든 벡터는 e1과 e2의 선형 결합에 의해 생성됨

u = (x, y) = xe1 + ye2

u' = (x', y') = x(cos(theta), sin(theta)) + y(-sin(theta), cos(theta))
    = (xcos(theta) - ysin(theta), xsin(theta) + ycos(theta))

삼각함수의 역함수

벡터의 좌표로부터 대응하는 각도를 얻을 때 삼각함수의 역함수를 활용

벡터의 각도를 얻을 때 tan의 역함수인 arctan 함수를 사용

• tan(theta) = y/x 이므로 이 값을 arctan에 넣으면 x축과 이루는 사잇각을 알 수 있음

tan 함수는 -90'와 90'일 때 y 값이 존재하지 않으므로 전단사함수가 되기 위한 정의역 구간은 (-90', 90')

따라서 각의 범위에 한계가 있는데, x와 y 값을 따로 전달하여 벡터가 존재하는 사분면을 파악해 각도를 계산하는 atan2(y, x) 함수를 사용

• 공역 구간은 (-180', 180')

극좌표계

동심원의 형태로 평면의 모든점을 표현하며, 주로 시간에 따른 회전의 움직임을 구현하거나 회전에 관련된 효과를 연출할 때 활용

데카르트 좌표계로 회전하면 회전에 따른 x와 y의 변화를 매번 계산하는 번거로움을 해결

극좌표계는 회전 동작을 기반으로 설계된 좌표계를 의미

원점으로부터의 거리 r과 각 theta 두 요소로 구성되며 (r, theta)

데카르트 좌표계 -> 극좌표계

r = sqrt(x^2 + y^2)

theta = atan2(y, x)

극좌표계 -> 데카르트 좌표계

x = rcos(theta)

y = rsin(theta)

데카르트 좌표계

직선의 수 집합을 수직으로 배치해 평면을 표기하는 방식

데카르트 좌표계의 한 원소는 곱집합과 동일하게 순서쌍으로 표현하며 좌표라고 부름

(x, y)

벡터 공간과 벡터

스칼라와 벡터

두 개 이상의 실수를 곱집합으로 묶어 공리적 집합론의 관점에서 규정한 것을 벡터 공간이라고 하며, 벡터 공간의 원소를 벡터라고 함

특정한 수 집합을 지칭하지 않고 연산이 갖는 성질만 다루기 때문에 좌표값은 체 집합의 원소로 규정

체의 구조를 가지는 수 집합의 원소를 스칼라라고 부름

벡터는 v = (x, y)로 표기함

벡터의 결합과 생성

선형 결합

선형 연산을 사용해 n개의 스칼라와 n개의 벡터를 결합해 새로운 벡터 v'를 생성하는 수식

a1v1 + a2v2 + ... + anvn = v'

모든 a가 0이 아님에도 영벡터를 생성한다면 선형 결합에 사용된 벡터는 서로 선형 종속의 관계를 가짐

영벡터를 생성하기 위해 모든 a가 0이어야 한다면 선형 결합에 사용된 벡터는 서로 선형 독립의 관계를 가짐

선형 독립의 관계를 가지는 벡터를 선형 결합하면 모든 벡터를 생성할 수 있기 때문에 벡터 공간을 다룰 때 선형적 관계가 중요

• 서로 평행하지 않은 두 개의 벡터만 가능

기저 : 벡터 공간 내 모든 벡터를 생성할 수 있는 선형 독립 관계를 가지는 벡터의 집합

기저벡터 : 기저에 속한 원소

표준기저 : 한 축만 사용하는 단위 벡터 (1, 0), (0, 1)로 구성된 직합

표준기저벡터 : 표준기저의 각 원소

기저벡터를 다른 값으로 변경하면 기저벡터로부터 세워진 벡터 공간의 모든 원소가 바뀌는데, 이는 선형 변환의 원리

평면으로 구성된 벡터 공간을 생성하기 위한 기저는 많지만 기저 집합의 수는 언제나 2개 뿐이므로, 평면에 대응되는 벡터 공간을 2차원으로 정의할 수 있음

벡터의 공간의 차원에는 제약이 없기 때문에 무한 확장이 가능

수와 집합

공리 : 명제 중에서 증명할 필요가 없는 기본 명제

공리적 집합론 : 공리를 기반으로 대상을 구분하는 집합론

• 공리적 집합론에서는 수가 가지는 연산에 대한 공리를 기반으로 수를 분류

수집합의 대표적인 연산으로는 사칙연산이 있으며, 이들을 두 개의 원소를 사용해 새로운 원소를 만들어내기 때문에 이항연산(Binary Operation)이라고도 함

이항연산의 성질

• 닫혀 있음 : 어떤 집합에서 두 원소를 사용한 이항연산의 결과가 항상 그 집합에 속하는 성질
• 교환 법칙 : 순서에 관계없이 항상 동일한 결과가 나오는 성질을 말함
  a + b = b + a
• 결합 법칙 : 연산이 두 번 이상 연속될 때, 앞의 연산을 먼저 계산한 결과와 뒤의 연산을 계산한 결과가 같은 성질
  (a + b) + c = a + (b + c)
• 분배 법칙 : 서로 다른 2가지 연산에 대해 다음의 규칙이 성립
  a(b + c) = ab + bc
• 항등원 : 임의의 수와의 연산 결과를 항상 동일한 수로 만들어주는 특별한 수
  a + 0 = a, 0은 덧셈의 항등원
  a * 1 = a, 1은 곱셈의 항등원
• 역원 : 임의의 수와의 연산 결과를 항상 항등원으로 만들어주는 특별한 수
  a + (-a) = 0, -a는 a의 덧셈 역원
  a * 1/a = 1, 1/a는 a의 덧셈 역원

체 : 11개의 공리를 모두 만족하는 수 집합

• 연산에 대해 닫혀있음
• 연산에 대해 결합법칙이 성립
• 연산에 대한 항등원이 존재
• 연산에 대한 역원이 존재
• 연산에 대해 교환 법칙이 성립
• 두 번째 연산에 대해 닫혀 있음
• 두 번째 연산에 대해 결합법칙이 성립
• 첫 번째 연산과 두 번째 연산에 대해 분배법칙이 성립
• 두 번째 연산에 대해 교환 법칙이 성립
• 두 번째 연산에 대해 항등원이 존재
• 두 번째 연산에 대해 역원이 존재(단 0은 제외)

실수는 유리수와 무리수를포함하여 완벽한 연속성을 가지는 직선을 만들어내는 수

실수를 대응시켜 표현한 직선을 수직선이라고 함

하나의 실수를 시각화할 때는 수직선의 고유한 위치에 점을 찍어 표현

수가 지니는 방향의 속성은 부호를 사용해 나타내며, 크기의 속성은 원점으로부터의 거리를 의미

함수

함수(Function)란 두 집합에서 첫 번째 집합(정의역)의 모든 원소(Input)가 빠짐없이 두 번째 집합(공역)의 어떤 원소(Output)에 대응하는 관계를 의미

• 정의역의 원소는 공역의 한 원소에만 대응돼야 함

치역은 정의역에 대응되는 공역의 원소만 형성된 부분 집합

2개의 함수를 연쇄적으로 이어서 하나의 함수로 만드는 연산을 함수의 합성이라 함

역함수는 어떤 함수와 합성한 결과가 언제나 항등한 함수