벡터(vector)
벡터는 크기와 방향을 모두 가진 수량을 가리킴
크기와 방향을 모두 가진 수량을 벡터값 수량이라고 부름
벡터는 힘이나 변위 속도(velocity), 3차원 게임에서 플레이어가 바라보는 방향, 다각형이 향한 방향, 광선이 이동하는 방향, 표면에서 광선이 반사되는 방향 등에 사용됨
벡터는 지향(방향이 있는) 선분으로 표시하는데, 선분의 길이는 벡터의 크기를 나타내고 선분 끝의 화살표는 벡터의 방향을 의미

벡터는 위치를 바꾸어도 벡터의 크기나 방향은 변하지 않기 때문에 위치는 중요하지 않음
따라서 두 벡터는 오직 길이가 같고 같은 방향을 가리킬 때 상등함
그래서 벡터를 다른 곳으로 이동해도 벡터의 의미는 변하지 않음
컴퓨터는 벡터들을 기하학적으로 다루지 못하므로 벡터들을 수치적으로 지정하는 방법이 필요한데, 이를 위해 공간에 하나의 3차원 좌표계를 도입하고, 모든 벡터의 꼬리를 원점으로 이동시키면 벡터를 머리(화살표 끝)의 좌표로 규정할 수 있으며, 벡터를 v = (x, y, z)로 표기할 수 있음

같은 벡터라도 좌표계가 다르다면 좌표 표현이 달라짐
위 문장이 중요한 이유는 어떤 벡터를 좌표로 규정하거나 식별할 때 항상 좌표계에 상대적임을 뜻하기 때문이다
3차원 컴퓨터 그래픽에서는 여러 개의 좌표계를 사용하는 경우가 많아 벡터를 다룰 때에는 벡터가 어떤 좌표계에 상대적인지를 기억해야 하고, 다른 좌표계로 변환하는 방법도 알아야 함

왼손잡이 좌표계는 DirectX, Unreal에서 사용하고, 오른손잡이 좌표계는 Unity에서 사용
양의 Z축 방향이 다른 것을 기억해야 함
기본적인 벡터 연산
두 벡터를 u = (x1, y1, z1), v = (x2, y2, z2)라고 가정하자
상등 : x1==x2 && y1==y2 && z1==z2일 때 u = v
덧셈 : u + v = (x1+x2, y1+y2, z1+z2)
기하학적으로 표현했을 때 u의 꼬리가 v의 머리와 일치하도록 이동했을 때 u'의 머리를 가리키는 벡터

스칼라(실수) 곱셈 : k*u = (kx1, ky1, kz1)
뺼셈 : u - v = u + (-1 * k) = u + (-v) = (x1-x2, y1-y2, z1-z2)
기하학적으로 표현했을 때 u의 머리에서 v의 머리로 향하는 벡터
그래픽 프로그래밍에서는 한 점에서 다른 점을 가리키는 벡터를 구해야하는 경우가 많음
u와 v를 점으로 간주할 때 v-u의 길이가 u에서 v까지의 거리라는 의미

영(zero) 벡터는 성분들이 모두 0인 벡터
벡터의 크기(길이)는 이중 수직선으로 표기(||u||)
x, y, z축은 서로 수직이기 때문에 직각삼각형 2개로 나눌 수 있음



벡터를 방향을 나타내는 용도로만 사용하는 경우에는 벡터의 길이가 중요하지 않기 때문에 벡터의 길이를 단위 길이(1)로 맞추는 것이 편리하다
따라서 벡터의 길이를 단위 길이인 단위 벡터로 만드는 것을 벡터의 정규화라고 부름
벡터의 각 성분을 벡터의 크기로 나누면 벡터가 정규화되며 단위 벡터가 됨

내적
스칼라 값을 내는 벡터 곱셈의 일종

세타는 벡터 u와 벡터 v 사이의 각도
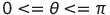
내적으로부터 이끌어낼 수 있는 유용한 기하학적인 속성
- 내적이 0이면 두 벡터는 수직(직교)
- 내적이 0보다 크면 두 벡터 사이의 각도는 90도 보다 작다
- 내적이 0보다 작으면 두 벡터 사이의 각도는 90보다 크다

벡터 v와 단위 벡터 n이 주어졌을 때 p를 내적을 이용해서 v와 n으로 표현해보자

이러한 p를 n에 대한 v의 직교투영(orthogonal projection)이라고 부름

정규 직교 집합 : 벡터들의 집합이 주어졌을 때, 벡터들이 서로 직교이고, 단위 길이인 벡터 집합
직교화 : 벡터들이 거의 정규 직교이지만 완전히 정규 직교가 아닐 때 직교 벡터 집합으로 만드는 것
일반적인 경우, n개의 벡터들의 집합을 직교화하는 경우에는 그람-슈미트 직교화 과정을 한다
기본 단계 : w0 = v0으로 설정

정규화 단계 : wi = wi / ||wi||로 설정
현재 벡터를 직교 벡터 집합에 들어있는 다른 벡터들의 방향으로의 부분을 빼서 직교가 되게 만듦
외적
벡터 곱셈으로, 두 벡터 모두에 직교인 벡터가 결과로 나옴
3차원 벡터에 대해서만 정의됨(2차원 벡터의 외적은 없음)
w = u x v = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)
왼손 좌표계일 경우 왼손 엄지 법칙 : 왼손으로 두 벡터의 방향을 검지와 중지로 가리켰을 때 엄지가 가리키는 방향
오른손 좌표계일 경우 오른손 엄지 법칙 : 오른손으로 두 벡터의 방향을 검지와 중지로 가리켰을 때 엄지가 가리키는 방향
u x v != v x u이므로 외적에 교환법칙이 적용되지 않음
u x v = - v x u
2차원 유사 외적
u = ( x, y )일 때 u에 수직인 벡터 v = ( -y, x ) = ( y, -x )
내적으로 수직을 증명하여 -xy + xy = xy - xy = 0
외적을 이용한 직교화
1. w0 = v0 / ||v0||
2. w2 = ( w0 x v1 ) / ( ||w0 x v1|| )
3. w1 = w2 x w0
점
지금까지의 벡터는 위치를 서술하지 않는데, 3차원 그래픽 프로그램에서는 3차원 기하구조의 위치나 3차원 가상 카메라의 위치 등, 공간 안의 어떤 위치를 지정할 수 있어야 함
특정한 좌표계를 기준으로 한 표준 위치에 있는 벡터(위치 벡터)를 3차원 공간 안의 한 위치를 나타내는 데 사용
위치 벡터에서 중요한 것은 위치를 나타내는 벡터의 머리 끝 좌표
위치 벡터만으로도 하나의 점을 규정하는 데 충분하므로 이 책에서는 위치 벡터와 점을 같은 의미로 사용
점을 벡터로 표현하는 장점은 두 점의 뺄셈이나, 점과 벡터를 더할 때 점의 위치도 특정한 좌표계에 상대적이지만 벡터 대수 자체에 그러한 개념이 있기 때문에 추가적인 작업을 해줄 필요가 없는 점
DirectXMath 라이브러리의 벡터 관련 기능
책에서는 XNA Math 라이브러리로 설명하고 있지만 DirectXMath로 마이그레이션됐으므로 DirectXMath로 표현
Code Migration from the XNA Math Library - Win32 apps
This overview describes the changes required to migrate existing code using the XNA Math library to the DirectXMath library.
learn.microsoft.com
Windows와 XBox 360에서 사용 가능한 특별한 하드웨어 레지스터들을 활용
Windows의 경우 SSE2(Streaming SIMD Extension 2) 명령 집합을 사용하여 128비트 너비의 SIMD(Single Instruction Multiple Data) 레지스터들을 이용해서 한 명령에서 32비트 float나 int 4개를 한 번에 처리할 수 있어 벡터 계산에 유용
예를 들어, 벡터의 덧셈을 계산할 때 하나의 SIMD 명령으로 2개의 SIMD 레지스터를 사용해 계산할 수 있음
코드에서 DirectXMath 라이브러리를 사용하려 할 때 모든 코드가 헤더 파일 안에 인라인으로 구현되어 있으므로 따로 라이브러리 파일을 링크할 필요 없이 헤더 파일을 포함시키면 됨
#include <DirectXMath.h>
벡터 타입들
핵심 벡터 타입은 SIMD 하드웨어 레지스터들에 대응되는 XMVEXTOR
#if defined(_XM_SSE_INTRINSICS_) && !defined(_XM_NO_INTRINSICS_)
using XMVECTOR = __m128;
#elif defined(_XM_ARM_NEON_INTRINSICS_) && !defined(_XM_NO_INTRINSICS_)
using XMVECTOR = float32x4_t;
#else
using XMVECTOR = __vector4;
#endif
XMVector는 16바이트 경계에서 정렬되어야 하는데, 지역 변수와 전역 변수에서는 정렬이 자동으로 이루어지고, 멤버의 경우는 XMFLOAT2(2차원)이나 XMFLOAT3(3차원), XMFLOAT4(4차원)을 사용하는 것이 바람직
그러나 XMFLOAT2 타입들을 계산에 직접 사용하면 SIMD의 장점을 취하지 못하는데, XMVECTOR 타입으로 변환하기 위해 Load 함수를 사용해야 함
적재 및 저장 함수들
XMFLOAT*를 XMVECTOR에 적재하는 함수
XMVECTOR XM_CALLCONV XMLoadFloat2(_In_ const XMFLOAT2* pSource) noexcept;
XMVECTOR XM_CALLCONV XMLoadFloat3(_In_ const XMFLOAT3* pSource) noexcept;
XMVECTOR XM_CALLCONV XMLoadFloat4(_In_ const XMFLOAT4* pSource) noexcept;
XMVECTOR의 자료를 XMFLOAT*로 저장하는 함수
void XM_CALLCONV XMStoreFloat2(_Out_ XMFLOAT2* pDestination, _In_ FXMVECTOR V) noexcept;
void XM_CALLCONV XMStoreFloat3(_Out_ XMFLOAT3* pDestination, _In_ FXMVECTOR V) noexcept;
void XM_CALLCONV XMStoreFloat4(_Out_ XMFLOAT4* pDestination, _In_ FXMVECTOR V) noexcept;
XMVECTOR 인스턴스의 성분을 읽거나 변경하는 함수
float XM_CALLCONV XMVectorGetX(FXMVECTOR V) noexcept;
float XM_CALLCONV XMVectorGetY(FXMVECTOR V) noexcept;
float XM_CALLCONV XMVectorGetZ(FXMVECTOR V) noexcept;
float XM_CALLCONV XMVectorGetW(FXMVECTOR V) noexcept;
XMVECTOR XM_CALLCONV XMVectorSetX(FXMVECTOR V, float x) noexcept;
XMVECTOR XM_CALLCONV XMVectorSetY(FXMVECTOR V, float y) noexcept;
XMVECTOR XM_CALLCONV XMVectorSetZ(FXMVECTOR V, float z) noexcept;
XMVECTOR XM_CALLCONV XMVectorSetW(FXMVECTOR V, float w) noexcept;
매개변수 전달
SIMD의 장점을 취하려면 함수에 XMVECTOR 타입의 매개변수를 전달할 때 지켜야 할 규칙이 있는데 이 규칙들은 플랫폼 마다 다름
플랫폼 독립적인 코드를 위해 CXMVECTOR과 FXMVECTOR 타입을 사용해야 함
차이는 값 타입과 참조자 타입
// Fix-up for (1st-3rd) XMVECTOR parameters that are pass-in-register for x86, ARM, ARM64, and vector call; by reference otherwise
#if ( defined(_M_IX86) || defined(_M_ARM) || defined(_M_ARM64) || _XM_VECTORCALL_ || __i386__ || __arm__ || __aarch64__ ) && !defined(_XM_NO_INTRINSICS_)
typedef const XMVECTOR FXMVECTOR;
#else
typedef const XMVECTOR& FXMVECTOR;
#endif
// Fix-up for (4th) XMVECTOR parameter to pass in-register for ARM, ARM64, and vector call; by reference otherwise
#if ( defined(_M_ARM) || defined(_M_ARM64) || defined(_M_HYBRID_X86_ARM64) || defined(_M_ARM64EC) || _XM_VECTORCALL_ || __arm__ || __aarch64__ ) && !defined(_XM_NO_INTRINSICS_)
typedef const XMVECTOR GXMVECTOR;
#else
typedef const XMVECTOR& GXMVECTOR;
#endif
// Fix-up for (5th & 6th) XMVECTOR parameter to pass in-register for ARM64 and vector call; by reference otherwise
#if ( defined(_M_ARM64) || defined(_M_HYBRID_X86_ARM64) || defined(_M_ARM64EC) || _XM_VECTORCALL_ || __aarch64__ ) && !defined(_XM_NO_INTRINSICS_)
typedef const XMVECTOR HXMVECTOR;
#else
typedef const XMVECTOR& HXMVECTOR;
#endif
한 함수의 처음 세 개의 XMVECTOR 매개변수는 반드시 FXMVECTOR 타입이어야 하고, 4번째와 5번째 매개변수는 GXMVECTOR 타입이어야 하고, 그 이후의 매개변수는 HXMVECTOR 타입이어어야 함
매개변수 사이에 XMVECTOR가 아닌 매개변수가 끼어 있을 수도 있음
XMMATRIX XM_CALLCONV XMMatrixTransformation2D(FXMVECTOR ScalingOrigin, float ScalingOrientation, FXMVECTOR Scaling, FXMVECTOR RotationOrigin, float Rotation, GXMVECTOR Translation) noexcept;
상수 벡터
const XMVECTOR 인스턴스에는 반드시 XMVECTORF32 타입을 사용해야 함
즉, 초기화 구문을 사용할 때 XMVECTORF32를 사용해야 함
XMGLOBALCONST XMVECTORF32 g_XMSinCoefficients0 = { { { -0.16666667f, +0.0083333310f, -0.00019840874f, +2.7525562e-06f } } };
XMVECTORF32는 16바이트 경계로 정렬된 구조체로, XMVECTOR로의 변환 연산자를 지원
XM_ALIGNED_STRUCT(16) XMVECTORF32
{
union
{
float f[4];
XMVECTOR v;
};
inline operator XMVECTOR() const noexcept { return v; }
inline operator const float* () const noexcept { return f; }
#ifdef _XM_NO_INTRINSICS_
#elif defined(_XM_SSE_INTRINSICS_)
inline operator __m128i() const noexcept { return _mm_castps_si128(v); }
inline operator __m128d() const noexcept { return _mm_castps_pd(v); }
#elif defined(_XM_ARM_NEON_INTRINSICS_) && defined(__GNUC__)
inline operator int32x4_t() const noexcept { return vreinterpretq_s32_f32(v); }
inline operator uint32x4_t() const noexcept { return vreinterpretq_u32_f32(v); }
#endif
};
오버로딩된 연산자들
XMVECTOR에는 벡터 덧셈, 뺄셈, 스칼라 곱셈을 위해 오버로딩된 연산자들이 있음
연산자 오버로딩을 비활성화하고 싶으면 매크로 상수 XM_NO_OPERATOR_OVERLOADS를 정의
#ifndef _XM_NO_XMVECTOR_OVERLOADS_
XMVECTOR XM_CALLCONV operator+ (FXMVECTOR V) noexcept;
XMVECTOR XM_CALLCONV operator- (FXMVECTOR V) noexcept;
XMVECTOR& XM_CALLCONV operator+= (XMVECTOR& V1, FXMVECTOR V2) noexcept;
XMVECTOR& XM_CALLCONV operator-= (XMVECTOR& V1, FXMVECTOR V2) noexcept;
XMVECTOR& XM_CALLCONV operator*= (XMVECTOR& V1, FXMVECTOR V2) noexcept;
XMVECTOR& XM_CALLCONV operator/= (XMVECTOR& V1, FXMVECTOR V2) noexcept;
XMVECTOR& operator*= (XMVECTOR& V, float S) noexcept;
XMVECTOR& operator/= (XMVECTOR& V, float S) noexcept;
XMVECTOR XM_CALLCONV operator+ (FXMVECTOR V1, FXMVECTOR V2) noexcept;
XMVECTOR XM_CALLCONV operator- (FXMVECTOR V1, FXMVECTOR V2) noexcept;
XMVECTOR XM_CALLCONV operator* (FXMVECTOR V1, FXMVECTOR V2) noexcept;
XMVECTOR XM_CALLCONV operator/ (FXMVECTOR V1, FXMVECTOR V2) noexcept;
XMVECTOR XM_CALLCONV operator* (FXMVECTOR V, float S) noexcept;
XMVECTOR XM_CALLCONV operator* (float S, FXMVECTOR V) noexcept;
XMVECTOR XM_CALLCONV operator/ (FXMVECTOR V, float S) noexcept;
#endif /* !_XM_NO_XMVECTOR_OVERLOADS_ */
기타 상수 및 함수
근삿값과 관련된 상수
constexpr float XM_PI = 3.141592654f;
constexpr float XM_2PI = 6.283185307f;
constexpr float XM_1DIVPI = 0.318309886f;
constexpr float XM_1DIV2PI = 0.159154943f;
constexpr float XM_PIDIV2 = 1.570796327f;
constexpr float XM_PIDIV4 = 0.785398163f;
라디안 단위 각도와 도(degree) 단위 각도의 변환을 위한 인라인 함수
constexpr float XMConvertToRadians(float fDegrees) noexcept { return fDegrees * (XM_PI / 180.0f); }
constexpr float XMConvertToDegrees(float fRadians) noexcept { return fRadians * (180.0f / XM_PI); }
최소값, 최대값을 위한 함수
template<class T> inline T XMMin(T a, T b) noexcept { return (a < b) ? a : b; }
template<class T> inline T XMMax(T a, T b) noexcept { return (a > b) ? a : b; }
설정 함수
XMVECTOR 객체의 내용을 설정하는 용도의 함수
XMVECTOR XM_CALLCONV XMVectorZero() noexcept; // 영벡터를 반환
XMVECTOR XM_CALLCONV XMVectorSplatOne() noexcept; // (1, 1, 1, 1) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorSet(float x, float y, float z, float w) noexcept; // (x, y, z, w) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorReplicate(float Value) noexcept; // (s, s, s, s) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorSplatX(FXMVECTOR V) noexcept; // (Vx, Vx, Vx, Vx) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorSplatY(FXMVECTOR V) noexcept; // (Vy, Vy, Vy, Vy) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorSplatZ(FXMVECTOR V) noexcept; // (Vz, Vz, Vz, Vz) 벡터 반환
XMVECTOR XM_CALLCONV XMVectorSplatW(FXMVECTOR V) noexcept; // (Vw, Vw, Vw, Vw) 벡터 반환
벡터 연산 함수
XMVECTOR XM_CALLCONV XMVector3Length(FXMVECTOR V) noexcept; // 벡터 길이 반환
XMVECTOR XM_CALLCONV XMVector3LengthSq(FXMVECTOR V) noexcept; // 벡터 길이 제곱 반환
XMVECTOR XM_CALLCONV XMVector3Dot(FXMVECTOR V1, FXMVECTOR V2) noexcept; // V1과 V2의 내적 반환
XMVECTOR XM_CALLCONV XMVector3Cross(FXMVECTOR V1, FXMVECTOR V2) noexcept; // V1과 V2의 외적 반환
XMVECTOR XM_CALLCONV XMVector2Orthogonal(FXMVECTOR V) noexcept; // V에 직교인 벡터 반환
XMVECTOR XM_CALLCONV XMVector2AngleBetweenVectors(FXMVECTOR V1, FXMVECTOR V2) noexcept; // 벡터 사이의 각도 반환
void XM_CALLCONV XMVector3ComponentsFromNormal(_Out_ XMVECTOR* pParallel, _Out_ XMVECTOR* pPerpendicular, _In_ FXMVECTOR V, _In_ FXMVECTOR Normal) noexcept; // projn(v), prepn(v) 반환
bool XM_CALLCONV XMVector3Equal(FXMVECTOR V1, FXMVECTOR V2) noexcept; // V1과 V2가 같은지 여부 반환
bool XM_CALLCONV XMVector3NotEqual(FXMVECTOR V1, FXMVECTOR V2) noexcept; // V1과 V2가 다른지 여부 반환
수학적으로 결과가 스칼라 값인 연산(예를 들면 내적)이라도 XMVECTOR를 반환하는 점에 주목
스칼라 결과는 XMVECTOR의 모든 성분에 복제되어 있음
이런 방식을 사용하는 이유는 계산 도중 모든 것을 SIMD로 유지하는 것이 더 효율적이기 때문에 스칼라 연산과 SIMD 벡터 연산의 전환을 최소화하기 때문
부동소수점 오차
벡터의 부동소수점 수를 비교할 때에 부동소수점의 부정확함을 반드시 고려해야 함
예를 들면 수학적으로는 정규화된 벡터의 길이가 정확히 1이어야 하지만 프로그램에서 벡터의 길이는 근사적으로 1이다.
부동소수점의 부정확함 때문에 두 부동소수점 수의 상등을 판정할 때에는 두 수가 근사적으로 같은지를 비교해야 함
bool XM_CALLCONV XMVector3NearEqual(FXMVECTOR V1, FXMVECTOR V2, FXMVECTOR Epsilon) noexcept;
'그래픽스 > DirectX 11을 이용한 3D 프로그래밍 입문' 카테고리의 다른 글
| [DirectX 11을 이용한 3D 게임 프로그래밍 입문] 3장 변환 (1) | 2025.02.25 |
|---|---|
| [DirectX 11을 이용한 3D 게임 프로그래밍 입문] 2장 행렬 대수 (0) | 2025.02.18 |