[DirectX 11을 이용한 3D 게임 프로그래밍 입문] 3장 변환

선형 변환

수학 함수 r(v) = r(x, y, z) = (x', y', z')

아래의 조건들을 만족하면 r을 가리켜 선형 변환(linear transformation)이라 부름

• r(u + v) = r(u) + r(v)
• r(ku) = kr(u)

 

u = (x, y, z) = xi + yj + zk = x(1, 0, 0) + y(0, 1, 0) + z(0, 0, 1)

i, j, k는 좌표계의 축들과 같은 방향인 단위벡터이고 이들을 표준기저벡터라고 부름

r(u) = r(xi + yj + zk) = xr(i) + y(j) + z(k)

위 식은 하나의 선형결합(일차결합)이므로 하나의 벡터 행렬 곱셈 형태로 표기할 수 있음

uA = [xA11 + yA21 + zA31, xA12 + yA22 + zA32, xA13 + yA23 + zA33]

     = [xA11, xA12, xA13] + [yA21 + yA22 + yA32] + [zA31 + zA32 + zA33]

     = xA1,* + yA2,* + zA3,*

r(i) = (A11, A12, A13), r(j) = (A21, A22, A23), r(k) = (A31, A32, A33)

이러한 행렬 A를 선형변환 r의 행렬 표현이라고 부름

 

비례

비례 변환은 다음과 같이 정의됨

S는 하나의 선형변환이므로 행렬 표현이 존재함

S(i) = (sx, 0, 0)

S(j) = (0, sy, 0)

S(k) = (0, 0, sz)

위 행렬을 비례 행렬이라고 함

 

회전

회전각은 축 n을 내려다 볼 때(머리에서 꼬리 쪽으로) 시계 방향으로 측정, ||n|| = 1이라고 가정

회전하려는 벡터 v를 n에 평행한 벡터 projn(v) = (nov)n와 n에 수직인 벡터 vㅗ = perpn(v) = v - projn(v)로 분할

n에 평행한 projn(v)는 축 n과 평행하므로 벡터가 회전해도 변하지 않기 때문에 수직인 부분을 회전하는 방법만 알면 됨

즉 회전된 벡터 Rn(v) = projn(v) + Rn(vㅗ)를 구하면 됨

|| n x v || = ||n||||v|| sina = ||v||sina = ||vㅗ||

vㅗ를 하나의 기준 벡터로 사용하고 n x v를 둘째 기준 벡터로 사용

(vㅗ는 v의 n에 수직인 성분이므로, n x v는 vㅗ에도 수직)

두 기준 벡터는 크기가 같고 회전의 원에 놓여 있음

 

Rn(v) = projn(v) + Rn(vㅗ)

 

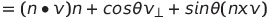
회전 행렬 Rn

(c = cos, s = sin)

 

회전행렬의 각 행벡터는 단위길이이고, 서로 직교이므로 행벡터들은 정규직교

직교행렬에는 역행렬이 자신의 전치행렬과 같은 속성이 있음

특히 회전축이 x축, y축, z축인 경우 회전행렬이 아주 간단해짐

 

아핀변환

동차좌표

아핀변환은 선형변환에 이동이 결합된 것

벡터는 위치와 무관하게 방향과 크기만 서술하는 것이므로 이동(위치벡터)는 점에만 적용되어야 하는데, 동차좌표를 이용하면 점과 벡터를 동일한 방식으로 다룰 수 있음

동차좌표는 3차원 벡터에 w 성분을 추가한 4원소쌍의 형태인데, 벡터의 경우 0이고 점의 경우 1

w = 1로 설정하면 이동 시 점이 정확이 이동되며 w = 0으로 설정하면 이동 시 벡터가 변하지 않음

 

정의 및 행렬 표현

아핀변환은 선형변환에 이동 벡터 b를 더한 것

a(u) = r(u) +b

 

w = 1인 동차좌표를 도입하면 간결하게 표기할 수 있음

 

이동

항등 변환 : 주어진 인수(입력)을 그대로 돌려주는 선형변환, I(u) = u

r(u) = uI + b = u + b

u를 b만큼 이동하므로 물체의 모든 점의 위치를 동일한 벡터 b로 이동

 

이동행렬

 

아핀변환 행렬의 기하학적 해석

r가 물체를 얼마나 회전할 것인지를 나타내는 회전 변환이고, b가 물체를 얼마나 이동할 것인지를 나타내는 이동 변환

a(x, y, z) = r(x, y, z) + b = xr(i) + yr(j) + zr(k) + b

r은 표준기저벡터 i, j, k만을 새로운 방향 r(i), r(j), r(k)로 회전

b는 원점으로부터의 변위를 나타내는 위치벡터

 

변환들의 합성

S가 비례행렬, R이 회전행렬, T가 이동행렬일 때 직육면체의 각 정점에 세 변환을 적용할 때 가장 직접적인 방법은 변환 행렬들을 단계별로 적용하는 것

((viS)R)T = vi(SRT)

 

여러 개의 변환들을 하나의 변환으로 결합할 수 있음

이는 성능에 영향을 미쳐 많은 변환들을 연달아 적용하면 n개의 점으로 이루어진 물체를 변환할 때 벡터 행렬 곱셈 n x 3회이지만 결합된 행렬 접근 방식은 벡터 행렬 곱셈 n + 행렬 행렬 곱셈 2회이므로 계산 횟수가 크게 줄어듦

 

좌표 변경 변환

한 좌표계의 상대적인 점 또는 벡터의 좌표를 다른 좌표계의 좌표로 변환하는 것

기하 구조 자체가 바뀌는 것이 아닌 좌표 표현이 변경되는 것

 

벡터

좌표계 A에서 B로 변환한다고 가정

Pa = xu + yv (u와 v는 x축과 y축 방향의 단위벡터)

 

벡터  u와 v의 b 기준 좌표를 알 수 있다면 다른 좌표계에 상대적인 좌표로 변환할 수 있음

Pb = xub + yvb = xub + yvb

 

점

점의 경우 위치가 중요하므로 벡터를 이동시키는 방식으로 점을 이동할 수는 없음

Pb = xub + yvb + Qb (Qb는 B의 원점에서 A 좌표계의 원점을 가리키는 벡터)

 

행렬 표현

벡터와 점에 대한 좌표 변경 변환을 동차좌표로 하나의 공식으로 처리할 수 있음

(x', y', z', w) = xub + yvb + zwb + wQb

w가 0이면 벡터에 대한 좌표 변경 변환을 의미하고 w가 1이면 점에 대한 좌표 변경 변환을 의미

 

좌표 변경 행렬 또는 좌표계 변환 행렬 또는 좌표 변환 행렬

 

결합 법칙과 좌표 변경 행렬

세 개의 좌표계 F, G, H가 있고 A가 F->G 좌표계 변환 행렬, B가 G->H 좌표계 변환 행렬

(PFA)B = PH

 

결합 법칙을 이용

PF(AB) = PH

C = AB는 F에서 H로 가는 좌표계 변환 행렬이라고 생각할 수 있음(함수의 합성과 비슷)

이는 성능에 영향을 미쳐 많은 변환들을 연달아 적용하면 n개의 점으로 이루어진 물체를 변환할 때 벡터 행렬 곱셈 n x 2회이지만 결합된 행렬 접근 방식은 벡터 행렬 곱셈 n + 행렬 행렬 곱셈 1회이므로 계산 횟수가 크게 줄어듦

 

역행렬과 좌표 변경 행렬

M이 좌표계 A에서 B로의 좌표 변경 행렬이고, 가역행렬(역행렬이 존재)하다고 가정

• 이 책에서 다루는 모든 좌표계 변환에서는 항상 역행렬이 존재

Pb = PaM

pbM^(-1) = PaMM^(-1) = PaI = Pa

따라서 M^(-1)은 B에서 A로의 좌표 변경 행렬

 

DirectXMath 라이브러리 관련 함수들

XMMATRIX    XM_CALLCONV     XMMatrixScaling(float ScaleX, float ScaleY, float ScaleZ) noexcept; // 비례행렬 생성
XMMATRIX    XM_CALLCONV     XMMatrixScalingFromVector(FXMVECTOR Scale) noexcept; // 벡터의 성분들로 비례행렬 생성

XMMATRIX    XM_CALLCONV     XMMatrixRotationX(float Angle) noexcept; // x축에 대한 회전행렬 Rx 생성
XMMATRIX    XM_CALLCONV     XMMatrixRotationY(float Angle) noexcept; // y축에 대한 회전행렬 Ry 생성
XMMATRIX    XM_CALLCONV     XMMatrixRotationZ(float Angle) noexcept; // z축에 대한 회전행렬 Rz 생성
XMMATRIX    XM_CALLCONV     XMMatrixRotationAxis(FXMVECTOR Axis, float Angle) noexcept; // 임의의 축에 대한 회전행렬 Rn 생성

XMMATRIX    XM_CALLCONV     XMMatrixTranslation(float OffsetX, float OffsetY, float OffsetZ) noexcept; // 이동행렬 생성
XMMATRIX    XM_CALLCONV     XMMatrixTranslationFromVector(FXMVECTOR Offset) noexcept; // 벡터의 성분들로 이동행렬 생성

XMVECTOR    XM_CALLCONV     XMVector3Transform(FXMVECTOR V, FXMMATRIX M) noexcept; // 벡터 행렬 곱 vM 계산
XMVECTOR    XM_CALLCONV     XMVector3TransformCoord(FXMVECTOR V, FXMMATRIX M) noexcept; // 벡터 행렬 곱 vM 계산, 점 변환을 위해 Vw = 1이 적용됨
XMVECTOR    XM_CALLCONV     XMVector3TransformNormal(FXMVECTOR V, FXMMATRIX M) noexcept; // 벡터 행렬 곱 vM 계산, 벡터 변환을 위해 Vw = 0이 적용됨
// 마지막 두 함수의 w 성분을 프로그래머가 직접 설정할 필요 없음